13 февраля 2024
Университетская олимпиада по математике «БЕЛЬЧОНОК»
Учащиеся 7-11 классов Образовательного центра «НИВА» приняли участие в отборочном этапе университетской олимпиады по математике «БЕЛЬЧОНОК» в январе 2024, по итогам которого семиклассник Москвин Михаил вышел в заключительный этап.
Поздравляем и желаем успехов в освоении царицы наук – математики!
Заключительный этап проводился 11 февраля в г. Москве на базе ФГБОУ ВО
«Национальный исследовательский университет «МЭИ».
Предлагаем вашему вниманию олимпиадные задания для 7 класса:
|
Задача 1 |
 |
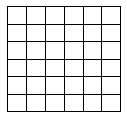| Расположите в каких-то клетках квадрата 6х6 по одной снежинке (*) так, чтобы в любой строке было ровно три снежинки, а в любом столбце – одна или четыре снежинки. |
|
Задача 2 |
| Есть мешок с орехами весом 1г, 2г, …, 50г и чашечные весы. Бельчата Вася и Петя по очереди кладут на весы по одному ореху из мешка, каждый на свою чашу, начинает Вася. После хода каждого игрока его чаша должна перевесить. Выигрывает тот, кто не сможет сделать очередной ход. Кто может выиграть, как бы ни играл соперник? |
|
Задача 3 |
Даша, Маша и Настя записали по натуральному числу. Даша умножила своѐ число на число Насти, а также свое число на число Маши; эти два произведения отличались друг от друга на 1. Маша умножила своѐ число на Дашино и своѐ на Настино; эти произведения отличались на 25. Наконец, Настя умножила своѐ число на Дашино и своѐ на число Маши. На сколько отличались произведения у Насти? Укажите все ответы и объясните, почему других нет. |
Олимпиада «Бельчонок» по предметам «математика» (III уровень), «информатика» (III уровень) и «химия» (II уровень) вошла в Перечень олимпиад школьников на 2023/24 учебный год под номером 85, утверждаемый Министерством науки и высшего образования Российской Федерации.Победа или призовое место по данному профилю олимпиады дает шанс воспользоваться льготами вуза (в соответствии с правилами приема) при условии, что выпускник подтвердит свой статус, набрав балл ЕГЭ по соответствующему общеобразовательному предмету не менее 75.